Логические уравнения
Краткая справка
Теоретический материал в полном объёме можно найти в работах [18,24,26].
Таблица базисных функций 4-значной комплементарной логики
| XY | X' | X&Y | X+Y | XY | X' | X&Y | X+Y |
| 00 | 1 | 0 | 0 | i0 | j | 0 | 1 |
| 0j | 1 | 0 | j | ij | j | 0 | 1 |
| 0i | 1 | 0 | i | ii | j | i | i |
| 01 | 1 | 0 | 1 | i1 | j | i | 1 |
| j0 | i | 0 | j | 10 | 0 | 0 | 1 |
| jj | i | j | j | 1j | 0 | j | 1 |
| ji | i | 0 | 1 | 1i | 0 | i | 1 |
| j1 | i | j | 1 | 11 | 0 | 1 | 1 |
Алгоритм "Селигер" решения логических уравнений
Практикум по решению логических уравнений
Задача 1
Дано : m = ab + cd = 1 --------------------------- Найти : d = f(a,b,c)
Решение
На основании исходного логического уравнения полной единицы строим таблицу истинности для разрешённых наборов, т.е. тех наборов, на которых исходное уравнение имеет решение. Перенеся столбцы a,b,c из исходной таблицы в качестве значений аргументов, а столбец d - в качестве значений искомой функции, получим таблицу истинности для d = f(a,b,c).
| dcba | _m_ |
| 0011 | 1 |
| 0111 | 1 |
| 1011 | 1 |
| 1111 | 1 |
| 1100 | 1 |
| 1101 | 1 |
| 1110 | 1 |
В соответствии с п.4 алгоритма "Селигер" построим диаграммы.
a =====================------=====----- b =====================-----------===== c ----=====------====================== d ---------============================
| cba | _d_ |
| 011 | 0 |
| 111 | 0 |
| 011 | 1 |
| 111 | 1 |
| 100 | 1 |
| 101 | 1 |
| 110 | 1 |
По полученной таблице заполним карту Карно, откуда после минимизации выведем соотношения для d = f(a,b,c). Если на некотором наборе функция принимает значение как 0, так и 1, то в соответствующую клетку карты Карно вписываем символ i. Если на каком либо наборе функция не определена, то в соответствующую клетку карты Карно вносим значение j. Здесь и далее апостроф означает отрицание аргумента или функции. Применение карты Карно не имеет принципиального значения : просто автор считает карты Карно наиболее эффективным инструментом для минимизации булевых функций.
| c \ ba | 00 | 01 | 11 | 10 |
| j | j | i | j | |
| 1 | 1 | i | 1 |
Клетки карты Карно с координатами 011 и 111 заполнены значением i, т.к. на этих наборах(индивидах,конституентах) d принимает значения как 0, так и 1. Наборы 000, 001 и 010 в таблице отсутствуют, поскольку при таких значениях аргументов исходное уравнение не имеет решения, поэтому соответствующие карты Карно заполнены символом j.
Для трёхзначной логики в этих клетках помещается прочерк, т.е. символ недоопределённости. Доопределение минимизируемой функции единицами позволяет получить компактную формулу.
Для комплементарной логики имеем:
d = cb' + ca' + iba + j(c'b' + c'a')
Для трёхзначной логики это уравнение выгдядит проще:
d = b' + a' + iba
Задача 2
Рассмотрим 1-ю задачу Порецкого[27]. Между птицами данного зоосада существует 5 отношений:
Определить, были ли птицы качества Х певчие или нет. Узнать то же в отношении птиц качества Y.Найти, были ли среди качества Х птицы качества Y и наоборот.
Решение
Пусть
Х - птицы качества Х. Y - птицы качества Y. S - певчие птицы. G - крупные птицы.
Тогда условие задачи будет представлено следующими рекурсивными уравнениями [27] :
1. s= (g+ у)s; 2. у'= (g'+x')у'; 3. s+g+x'=1; 4. g'=(s+x)g'; 5. xуs'g=0.
Эти уравнения Порецкий через эквивалентность приводит к единичной форме:
1. g+у+s'=1 2. g'+x'+у=1 3. s+g+x'=1 4. s+g+x=1 5. x'+у'+s+g'=1
Нетрудно заметить, что система уравнений Порецкого представляет из себя сорит, содержащий посылки общего характера(см. раздел 4). По соответствующим формулам из базиса Васильева преобразуем уравнения Порецкого:
1. g+у+s'=As(g+y). 2. g'+x'+у=Ay'(g'+x'). 3. s+g+x'=Ax(s+g). 4. s+g+x=Ag'(s+x). 5. x'+у'+s+g'=E(xy)(s'g).
Ктати, эта функторная мнемоника напрямую описывает текстовые посылки Порецкого. Порецким впервые в мире применены здесь многоаргументные функторы, о которых мечтал Л.Кэрролл. Порецкий также впервые в мире отыскал методы решения многоаргументных полисиллогизмов общего характера. Посылки частно-утвердительного характера метод Порецкого обрабатывать не может. У Кэрролла нет решения даже для многоаргументных соритов, не говоря уже о полисиллогизмах.
Полная логическая единица M всей задачи определится как конъюнкция всех левых частей системы логических уравнений. Эту рутинную операцию можно заменить на менее утомительную процедуру построения дизъюнкции нулей. Получим систему:
1. g'у's=0 2. gxу'=0 3. g's'x=0 4. g's'x'=0 5. gs'xу=0
Полный логический нуль системы равен дизъюнкции всех левых частей системы логических уравнений. Проведём решение задачи Порецкого с использованием карты Карно, а потом сопоставим результаты. Заполним карту Карно нулями в соответствии с нулевыми термами системы, а в оставшиеся клетки впишем единицы. Тогда полная логическая единица всей задачи после минимизации примет вид:
m=sу+gx'
| gs\xy | 00 | 01 | 11 | 10 |
| 00 | 0 | 0 | 0 | 0 |
| 01 | 0 | 1 | 1 | 0 |
| 11 | 1 | 1 | 1 | 0 |
| 10 | 1 | 1 | 0 | 0 |
Выпишем из карты Карно все единичные наборы в виде таблицы истинности. По полученной таблице построим таблицы для х=f1(g, s),y=f2(g,s) и у=f3(х). Если на каком-либо наборе функция принимает значение как 0, так и 1, то в соответствующую клетку карты Карно вписываем 1. Если какой-нибудь набор отсутствует, то для этого набора в карту Карно вносим значение j.
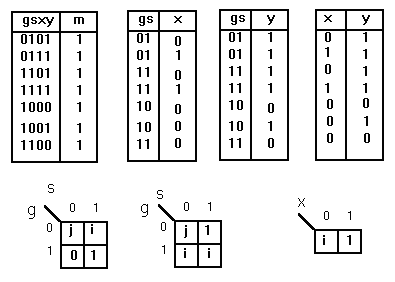
g -----------========================== s ======================----------===== x ----=======-----======--------------- y ======================-----=====----- 0101 0111 1101 1111 1000 1001 1100
После минимизации получим для комплементарной логики системы уравнений:
x = is + jg's' у = g's + ig + jg's' у = x + ix' = (x + ix) + ix' = x + i
Результаты, полученные Порецким:
x = xs у = gу + g's у = у + x
Из диаграмм и сокращённой таблицы истинности можно получить и более прозрачные результаты:
F1(x,s) = x'+s = Axs. F2(g,s,y) = sy+g = Ag'(sy) = A9s'+y')g. F3(x,y) = y+x' = Axy.
Задача 3
Рассмотрим 2-ю задачу Порецкого.
Относительно белья в комоде известны 2 положения:
Узнать, какое бельё было поношено: крупное или мелкое.
Решение
Пусть а - тонкое, b - крупное, с - дорогое, d - новое бельё. Тогда имеем следующую систему уравнний:
1. b + a(d' + c') = 1 2. (a' + d'c) = ab'c' + b(d + ac')
В соответствии с алгоритмом "Селигер" получим:
1. a'b' + b'cd = 0 2. a'b' + a'd' + cd' + 0
Нулевые термы системы уравнений занесём в карту Карно, откуда получим функцию полной единицы. По полученному соотношению строим сокращённую таблицу истинности и выписываем из неё значения b и d в виде таблицы, из которой получаем логическую функцию. Из этой функции следует, что d не зависит от b, что совпадает с результатом Порецкого.
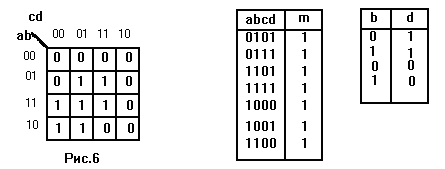
a -----------========================== b ======================----------===== c ----=======-----======--------------- d ======================-----=====----- 0101 0111 1101 1111 1000 1001 1100
По алгоритму "Селигер" получим b = i, а по алгоритму "ТВАТ"
f(b,d) = 1 = Ibd(8).
Эти выражения эквивалентны.
Задача 4
Дано: z = xу , v = x + у. ------------------------------ Найти: у = z/x , у = v-x .
Решение
На основе формулы эквивалентности преобразуем исходную формулу z=xу. Тогда получим (z=xу) = zxу + z'(x'+у'). В соответствии с пп.4, 5 алгоритма "Селигер" получим у = xz+ix'z'+jx'z.
Решим ту же задачу посредством алгоритма "Селигер-С". Исходные уравнения представим в виде таблицы истинности. Тогда в соответствии с п.2 алгоритма "Селигер-С" построим частные таблицы истинности для у= z/x и у=v-x.
| xy | z | v |
| 00 | 0 | 0 |
| 01 | 0 | 1 |
| 10 | 0 | 1 |
| 11 | 1 | 1 |
| xy | y=z/x |
| 00 | i |
| 01 | j |
| 10 | 0 |
| 11 | 1 |
| xy | y=v-x |
| 00 | 0 |
| 01 | 1 |
| 10 | j |
| 11 | i |
В соответствии с п.3 алгоритма "Селигер-С проведём минимизацию искомых функций в трёхзначной и комплементарной логиках.
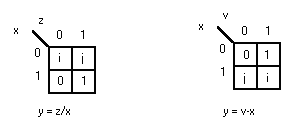
Для комплементарной логики получим:
у = z/x = xz + ix'z' + jx'z у = u-x = x'v + ixv + ixv'
Для трёхзначной логики уравнения имеют вид:
у = z/x = xz + ix' у = v-x = x'v + ix
Однозначным и более строгим решением являются уравнения комплементарной логики.
Задача 5
Дана система логических уравнений (В. С. Левченков "Булевы уравнения" - М.:1999 ):
ax = bc bx = ac -------------- Найти х.
Решение
Напрашивается простой и "очевидный" метод решения: сложить левые и правые части уравнений и сократить на общий множитель. В результате получим (a+b)x = (a+b)c. Откуда x = c, a = b. Ответ настораживает, тем более, что что решение противоречит принципу отыскания парных индивидов, поэтому проверим его на основе разработанных алгоритмов.
Действительно, сложить левые и правые части уравнений мы имеем право на основании правила (9П) Порецкого. Кстати, заодно и проверим это правило:
(9П) (e=c) -> (e+b=c+b) = ec'+e'c+(e+b)(c+b)+(e+b)'(c+b)' = = ec'+e'c+ec+b+e'b'c' = 1;
Да, Порецкий не ошибся. Однако относительно сокращения на общий множитель великий русский логик нам ничего не сообщил. А так хочется это сделать, тем более что всё очевидно, и обычная алгебра нам не запрещает подобные операции. Проверим допустимость сокращения на общий множитель с помощью алгоритма "Импульс":
(cx=cy) -> (x=y) = cx(cy)'+(cx)'cy+xy+x'y' = cxy'+cx'y+xy+x'y'№1.
Оказывается, что алгебра логики не разрешает нам этакие вольности, т.е. мы доказали, что уравнения (cx=cy) и (x=y) не равносильны.
По алгоритму "Селигер" :
M = (ax = bc)( bx = ac) M' = (axЕbc) + ( bxЕac) = = ab'x+ac'x+a'bc+bcx'+a'bx+bc'x+acx'+ab'c.
После занесения M'в карту Карно получим
M = a'b'+abcx+c'x'.
Откуда решение системы логических уравнений в соответствии с алгоритмом "Селигер" примет вид:
x = abc+ia'b'+jc(ab'+a'b). a = bcx+ic'x'+jb(cx'+c'x).
Заданная система уравнений может быть представлена графически при помощи скалярных диаграмм . Скалярные диаграммы построены по рабочим наборам таблицы истинности для М.
a -------------======----============== b -------------==========-------======= c --------===========------------------ x ---=====----=======------------------
Скалярные диаграммы дают полное представление о системе уравнений. Подтвердим корректность метода на решении более прозрачной задачи.
Задача 6
Дана система логических уравнений:
x = y u = v ------------------------- Найти решение системы.
Решение
M = (x = y)(u = v) = (xy + x'y')(uv + u'v') = = u'v'(x'y' + xy)+uv(x'y' + xy).
Для обеспечения наглядности решения уравнения представим полную единицу системы М в виде скалярных диаграмм.
| uvxy | _m_ |
| 0000 | 1 |
| 0011 | 1 |
| 1100 | 1 |
| 1111 | 1 |
u ----------------===================== v ----------------===================== x ------==========-----------========== y ------==========-----------==========
По алгоритму "Селигер" получим
y(x,u,v) = x(u = v)+j(u Е v)
Для перехода к y(x) достаточно в таблице истинности для полной единицы М вынести столбец значений y в графу функций и произвести синтез y(x) по вышеизложенным алгоритмам. Второй способ заключается в том, что в полученной формуле для y(x,u,v) мы заменим лишние аргументы u,v на 1. В результате мы подтвердим исходное уравнение системы y(x) = x. Аналогично можно показать,что u(v) = v.
Задача 7
Используя алгоритм "Селигер", получить полную систему обратных функций для двоичной логики. В таблице приведена полная система функций двоичной логики.
| xy | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 | z10 | z11 | z12 | z13 | z14 | z15 |
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 01 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 10 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 11 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
Решение
Перестановкой столбцов у и z исходной таблицы строим таблицу истинности для полной системы обратных функций.
| xz | y0 | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | z11 | z12 | z13 | z14 | z15 |
| 00 | I | i | i | i | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | j | j | j | j |
| 01 | J | j | j | j | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | i | i | i | i |
| 10 | I | 0 | 1 | j | i | 0 | 1 | j | i | 0 | 1 | j | i | 0 | 1 | j |
| 11 | J | 1 | 0 | i | j | 1 | 0 | i | j | 1 | 0 | i | j | 1 | 0 | i |
Из таблицы обратных функций получаем полную симметричную систему обратных функций y = f1(x,z),а по алгоритму "Селигер" - y = f2(x):
у0 = iz'+jz y0 = j у1 = xz+ix'z'+jx'z y1 = x+jx' у2 = xz'+ix'z'+jx'z y2 = jx' у3 = i(xz+x'z')+j(xz'+x'z) y3 = ix+jx' у4 = x'z+ixz'+jxz y4 = x'+jx у5 = z y5 = 1 у6 = xz'+x'z y6 = x' у7 = x'z+ixz+jxz' y7 = x'+ix у8 = x'z'+ixz'+jxz y8 = jx у9 = xz+x'z' y9 = x у10= z' y10 = 0 у11= x'z'+ixz+jxz' y11 = ix у12= i(xz'+x'z)+j(xz+x'z') y12 = ix'+jx у13= xz+ix'z+jx'z' y13 = x+ix' - импликация у14= xz'+ix'z+jx'z' y14 = ix' у15= iz+jz' y15 = i
Кстати, переход от левой системы уравнений к правой легко выполняется простой заменой z на 1 и z' на 0.