Синтез и минимизация логических функций

Краткая справка

Более подробный теоретический материал можно найти в [16,17,21,24]. Здесь и далее во всех формулах апостроф означает инверсию (отрицание).

Основные законы алгебры Буля:

а) Переместительный закон
     а + в = в + а ;                             ав = ва
б) Сочетательный закон
    ( а + в ) + с = а + ( в + с) ;               (ав)с = а(вс)
в) Распределительный закон
    а( в + с ) = ав + ас ;                       а + вс = (а + в)(а + с)
г) Закон поглощения
     а + ав = а( 1 + в ) = а ;                   а(а + в) = а + ав = а
д) Закон склеивания
     ав + ав' = а ;                              (а + в)(а + в') = а
е) Идемпотентный закон
     a + a = a;                                  a & a = a
ё) Правила де Моргана
     Эти правила справедливы для любого числа аргументов. 
     а + в + с + .... + z = ( а'в'с'...z' )'
     авс... = ( а' + в' + с' + ... + z' )'

Алгоритм "НИИРТА" графической минимизации булевых функций

1. Заполнить карту Карно нулями и единицами в соответствии с таблицей истинности или заданным алгебраическим выражением.
2. Покрыть все элементарные квадраты Карно, в которых записаны единицы, минимальным количеством фигур покрытия, каждая из которых имеет максимальную площадь.
3. Проверить каждую фигуру покрытия на соответствие принципу симметрии. В противном случае изменить контур фигуры покрытия в соответствии с принципом симметрии так, чтобы она превратилась в прямоугольник Карно.
4. Каждому прямоугольнику Карно соответствует одна импликанта, причём если в границах прямоугольника Карно какая-либо переменная принимает значения как 0 , так и 1 , то эта переменная не войдёт в импликанту.

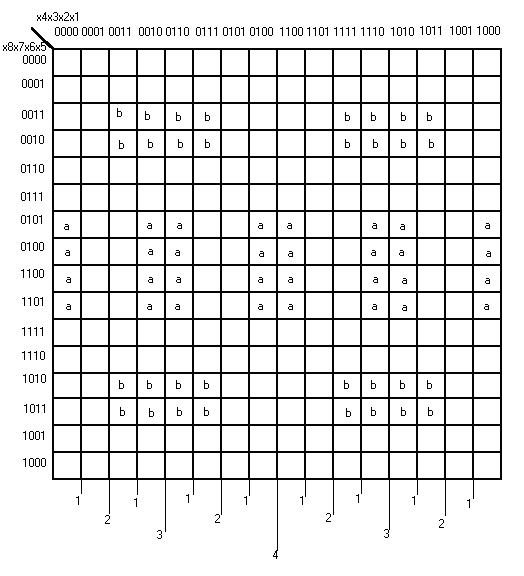
Карта Карно на 8 переменных с прямоугольниками Карно.

Алгоритм проверки достоверности прямоугольника Карно(принцип симметрии)

1. Если предполагаемый прямоугольник Карно (ППК) охватывает одну ось симметрии, либо не охватывает ни одной, то перейти к п.4.
2. Если ППК располагается по обе стороны от нескольких осей симметрии, то он должен быть симметричен относительно той из этих осей, которая имеет максимальный ранг, иначе данная фигура не является прямоугольником Карно.
3. Разбить исходный ППК пополам. Считать любую его половину новым ППК. Перейти к п.1.
4. Конец.

Этот алгоритм необходимо применить дважды: относительно горизонтальных и относительно вертикальных осей симметрии.

Практикум по синтезу и минимизации логических функций

Задача 1

Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется той группой, в которой оказался председатель приемной комиссии. Построить автомат, обеспечивающий определение большинства голосов.

Решение

Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае.

Обозначим через x4 голос председателя комиссии. x4 = 1, если председатель комиссии проголосовал за приём абитуриента. x3, x2, x1 - голоса членов приёмной комиссии.

С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности.

Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x1 - x4. Для n входных переменных существует N = 2n наборов переменных. В нашем Задачае N = 24 = 16 наборов.

Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.

x4
x3
x2
x1
_f_
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
0
0
1
0
0
1
1
1
0
1
0
1
1
0
1
1
1
1
1
0
0
1
1
1
0
1
1
1
1
1
0
1
1
1
1
1
1

Примечание. Здесь и далее под набором будем понимать конъюнкцию всех входных переменных. Существует множество научных определений для набора(конституента,терм,импликанта,минтерм и т.д.),но они только вносят путаницу.

Все наборы, на которых функция принимает значение 1 , будем называть единичными, или рабочими. Наборы, на которых функция принимает значение 0, будем называть нулевыми, или запрещенными.

Для того, чтобы по таблице истинности найти функцию f, достаточно выписать все единичные наборы и соединить их знаком дизъюнкции.

Таким образом,

f = x4'x3x2x1 + x4x3'x2'x1 + x4x3'x2x1' + x4x3'x2x1 +
  + x4x3x2'x1' + x4x3x2'x1 + x4x3x2x1' + x4x3x2x1                                                                                                                                                                              

Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), так как каждое логическое слагаемое представляет собой конъюнкцию всех аргументов.

Очевидно, применяя основные законы булевой алгебры, мы могли бы аналитически уменьшить сложность полученного выражения. Но это наихудший способ минимизации булевых функций. Покажем это на предыдущем Задачае. Представим полученную функцию в виде логической суммы цифровых рабочих наборов:

f = 0111+1001+1010+1011+1100+1101+1110+1111 = 
  = (0111+1111)+(1001+1011)+(1010+1011)+(1100+1101)+(1110+1111) = 
  = -111+10-1+101-+110-+111- = -111+10-1+(101-+111-)+(110-+111-) = 
  = -111+10-1+1-1-+11-- = x3x2x1+ x4x3'x1+ x4x2+ x4x3.

Как мы потом увидим, результат минимизации должен быть компактнее. Но при аналитической минимизации придётся ввести неочевидную группировку: (1101+1111).

f = 0111+1001+1010+1011+1100+1101+1110+1111 = 
  =(0111+1111)+(1001+1011)+(1010+1011)+
  +(1100+1101)+(1110+1111) + (1101+1111).= 
  = -111+10-1+101-+110-+111-+11-1 =
  = -111+(10-1+11-1)+(101-+111-)+(110-+111-) = 
  = -111+1--1+1-1-+11-- = x3x2x1+ x4x1+ x4x2+ x4x3 =
  = x3x2x1+ x4 (x1+ x2+ x3).

После длинных и неочевидных группировок удалось, наконец, получить правильное решение. При числе аргументов более 4-х аналитический метод минимизации не рационален.

Применим карту Карно для решения задачи 1. На рисунке даны два варианта решения.

f = x4x1 + x4x2 + x4x3 + x3x2x1                            
f' = x4'x1' + x4'x2' + x4'x3' + x3'x2'x1'                 

Эти выражения представляют собой Задача дизъюнктивной нормальной формы (ДНФ).

В некоторых случаях приведение результата минимизации к скобочной форме позволяет уменьшить количество ИС , необходимые для реализации булевой функции. Скобочная форма для f имеет вид:

f = x4(x1 + x2 + x3) + x3x2x1                               

Карта Карно для решения задачи 1.

Задача 2

Полностью определённая булева функция от 4-х переменных задана десятичными рабочими наборами : РН(4) = 5, 6, 7, 8, 9, 10, 11.Число в скобках указывает количество переменных. Найти минимальную форму этой функции.

Решение

Так как функция является полностью определённой, то запрещёнными наборами ЗН(4) являются наборы 0 - 4, 12 - 15. Исходя из этой информации, составляем таблицу истинности и осуществляем минимизацию по карте Карно.

Таблица 4

		

PH(4)
x4
x3
x2
x1
_f_
5
0
1
0
1
1
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
1
9
1
0
0
1
1
10
1
0
1
0
1
11
1
0
1
1
1




3H(4)
x4
x3
x2
x1
_f_
0
0
0
0
0
0
1
0
0
0
1
0
2
0
0
1
0
0
3
0
0
1
1
0
4
0
1
0
0
0
12
1
1
0
0
0
13
1
1
0
1
0
14
1
1
1
0
0
15
1
1
1
1
0

По карте Карно получаем результат:

f = x4x3' + x4'x3(x1 + x2)

Решение задачи 2

Задание 1.1

Найти минимальную форму полностью определённых булевых функций, заданных 10-чными рабочим наборами :

1. РН(4) = 0, 1, 5, 7 - 9, 13, 15
2. РН(5) = 4, 6, 8, 10, 13, 17, 24, 30
3. РН(6) = 1 - 8, 16 - 24, 32 - 40
4. РН(7) = 7 - 15, 23 - 31, 39 - 47, 50 - 63
5. РН(8) = 7 - 15, 100 - 132

Задача 3

Найти минимальную форму функции y, представленной на рисунке.

Решение

Функция задана только на 5 наборах. Добавим к трём рабочим наборам ещё пять, а именно : 0000, 0011, 1000, 1011, 1010. Все оставшиеся наборы доопределим как запрещённые. В результате такого доопределения получим прямоугольник Карно, состоящий из 8 элементарных квадратов Карно. Этому прямоугольнику соответствует функция :

   y = b'		

Решение задачи 3

Задача 4

Построить преобразователь двоичного кода, получаемого на выходе делителя частоты на 12, в двоично-десятичный код. Условие задачи отражено в таблице . Делитель работает в коде 8-4-2-1.

x4
x3
x2
x1
y5
y4
y3
y2
y1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
0
1
1
0
0
0
1
1
0
1
0
0
0
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
1
0
0
0
1
1
0
0
1
1
1
0
0
1
1
1
1
0
0
0
0
1
0
0
0
1
0
0
1
0
1
0
0
1
1
0
1
0
1
0
0
0
0
1
0
1
1
1
0
0
0
1

Решение

Для каждой функции yi заполняем карту Карно, производим доопределение и осуществляем минимизацию. Весь процесс отражён на рисунке.

В результате минимизации получаем систему функций:

y1 = x1 
y2 = x4'x2 
y3 = x3
y4 = x4x2'
y5 = x4x2
 

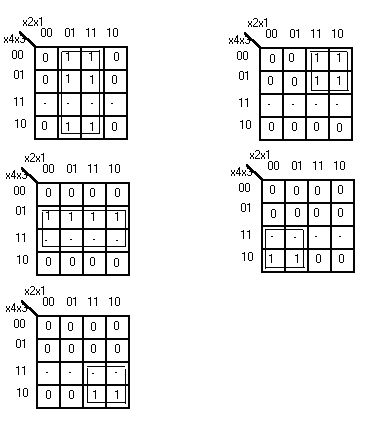
Карты Карно к задаче 4.

Задача 5

Построить один разряд многоразрядного сумматора.

Решение

Пусть ai и вi - значения i-ых разрядов слагаемых а и в , Pi и Si - значения переноса и суммы на выходе i-го разряда, Pi-1 - значение переноса на выходе предыдущего разряда, тогда работу сумматора можно описать с помощью таблицы истинности.

ai
bi
Pi-1
Pi
Si
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1

Имеем систему полностью определённых булевых функций. Производим раздельную минимизацию (см. рисунок).

Si = ai'вi'Pi-1 + ai'вiPi-1' + aiвi'Pi-1' + aiвiPi-1 =
   = Pi-1(ai~вi) + Pi-1'(aiЕ вi) = 
Pi = вiPi-1 + aiPi-1 + aiвi

Решение задачи 5

Для реализации лучше Pi = aiвi + Pi-1(ai~вi)' , так как может быть использован общий для Si и Pi сомножитель (аi~вi)'. Схема сумматора представлена на рисунке. Здесь же дано условное обозначение одноразрядного сумматора , где А и В - одноразрядные слагаемые, P0 и P1 - входной и выходной переносы, S1 - сумма.

На этом же рисунке изображён двухразрядный сумматор, выполненный на микросхеме 133ИМ2. Здесь А1, В1, А2, В2 - соответственно значения первых и вторых разрядов слагаемых А и В; S1 и S2 - 1-ый и 2-ой разряды суммы; P0 - входной перенос для первого разряда, P2' - выходной перенос.

Схемы сумматоров.

Задание 1.2

1. Построить 2/(2-10) преобразователь для делителя частоты на 24 , работающего в коде 16-8-4-2-1.
2. Построить 4-входовой сумматор для суммирования одноразрядных двоичных чисел.
3. Провести минимизацию автомата для тайного голосования методом обобщённых кодов.