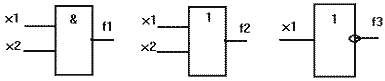
Вместо функции И часто используется термин "конъюнкция", вместо функции ИЛИ - термин "дизъюнкция". По ЕСКД логические элементы, реализующие функции И(f1), ИЛИ(f2), НЕ(f3), изображаются так, как представлено на рисунке.
Комбинационные логические цепи
Основные положения алгебры логики
Анализ и синтез логических схем осуществляется на базе аппарата алгебры логики или булевой алгебры [9]. Излагать весь аппарат не имеет смысла, так как в инженерной практике используются два-три закона алгебры логики.
В алгебре логики переменные могут принимать только два значения, 0 или 1. Для двух аргументов существуют 16 логических функций (операций, логических действий). Над переменными в основном производятся три логических действия: сложение, умножение, отрицание (инверсия), что соответствует функциям ИЛИ, И, НЕ. Все функции в булевой алгебре могут быть описаны с помощью таблицы истинности. В нижеследующих таблицах описаны функции И(f1), ИЛИ(f2),НЕ(f3).
| Аргументы | Функции | ||
| x2 | x1 | f1 | f2 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| Аргумент | Функция |
| x | f3 |
| 0 | 1 |
| 1 | 0 |
Вместо функции И часто используется термин "конъюнкция", вместо функции ИЛИ - термин "дизъюнкция". По ЕСКД логические элементы, реализующие функции И(f1), ИЛИ(f2), НЕ(f3), изображаются так, как представлено на рисунке.
При написании логических формул для функции И используются следующие знаки : &, U, точка или ее отсутствие; для функции ИЛИ +,^. Функция НЕ обозначается штрихом над аргументом. Мы для обозначения отрицания будем использовать апостроф. Таким образом, можно записать:
f1 = x2&x1 = x2^x1 = x2x1 f2 = x2Ux1 = x2+x1 f3 = x'
Основные законы алгебры Буля
Как уже отмечалось, в булевой алгебре все операции осуществляются с логическими переменными и подчиняются законам алгебры логики. Опишем некоторые из них.
а) Переместительный закон
а + в = в + а; ав = ва
б) Сочетательный закон
(а + в) + с = а + (в + с); (ав)с = а(вс)
в) Распределительный закон
а(в + с) = ав + ас; а + вс = (а + в)(а + с)
г) Закон поглощения
а + ав = а(1 + в) = а; а(a + в) = а + ав = а
д) Закон склеивания
ав + ав' = а; (а + в)(а + в') = а
е) Идемпотентный закон
a + a = a; a & a = a
ё) Правила де Моргана
Эти правила справедливы для любого числа аргументов.
а + в + с + .... + z = ( а'в'с'...z' )'
авс... = ( а' + в' + с' + ... + z' )'
Эти правила можно описать таким алгоритмом.
Для перехода от логической суммы к логическому произведению необходимо проделать следующие операции :
Аналогично выполняется переход от логического произведения к логической сумме.В инженерной практике используются лишь правила де Моргана и закон склеивания(в виде карт Карно).
Кроме основных функций И, ИЛИ, НЕ в алгебре логики часто используются функции равнозначности (эквивалентности) и неравнозначности (сумма по модулю 2 ).
Для обозначения этих функций используются следующие знаки : равнозначность - ~ , сумма по модулю 2 - 
. Содержание этих функций отражено в таблице .
| a | b | f4 | f5 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Из таблицы получаем:
f4 = а ~ в = а'в' + ав f5 = a
1.3. Синтез комбинационных схем
Синтез комбинационных схем можно проиллюстрировать решением простой задачи.
Задача 1
Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется той группой, в которой оказался председатель приемной комиссии. Построить автомат, обеспечивающий определение большинства голосов.
Решение
Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае.
Обозначим через x4 голос председателя комиссии. x4 = 1, если председатель комиссии проголосовал за приём абитуриента. x3, x2, x1 - голоса членов приёмной комиссии.
С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности.
Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x1 - x4. Для n входных переменных существует N = 2n наборов переменных. В нашем примере N = 24 = 16 наборов.
Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.
x4 x3 x2 x1 f 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1
Примечание
Здесь и далее под набором будем понимать конъюнкцию всех входных переменных. Существует множество научных определений для набора(конституента,терм,импликанта,минтерм и т.д.),но они только вносят путаницу.
Все наборы, на которых функция принимает значение 1 , будем называть единичными, или рабочими. Наборы, на которых функция принимает значение 0, будем называть нулевыми, или запрещенными.
Для того, чтобы по таблице истинности найти функцию f, достаточно выписать все единичные наборы и соединить их знаком дизъюнкции.
Таким образом,
f = x4'x3x2x1 + x4x3'x2'x1 + x4x3'x2x1' + x4x3'x2x1 + x4x3x2'x1' + x4x3x2'x1 +
+ x4x3x2x1' + x4x3x2x1
Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), так как каждое логическое слагаемое представляет собой конъюнкцию всех аргументов.
Очевидно, применяя основные законы булевой алгебры, мы могли бы аналитически уменьшить сложность полученного выражения. Но это наихудший способ минимизации булевых функций. Покажем это на предыдущем примере. Представим полученную функцию в виде логической суммы цифровых рабочих наборов:
f = 0111+1001+1010+1011+1100+1101+1110+1111 = = (0111+1111)+(1001+1011)+(1010+1011)+(1100+1101)+(1110+1111) = = -111+10-1+101-+110-+111- = -111+10-1+(101-+111-)+(110-+111-) = = -111+10-1+1-1-+11- = x3x2x1+ x4x3'x1+ x4x2+ x4x3.
Как мы потом увидим, результат минимизации должен быть компактнее. Но при аналитической минимизации придётся ввести неочевидную группировку: (1101+1111).
f = 0111+1001+1010+1011+1100+1101+1110+1111 = =(0111+1111)+(1001+1011)+(1010+1011)+(1100+1101)+(1110+1111) + (1101+1111).= = -111+10-1+101-+110-+111-+11-1 = -111+(10-1+11-1)+(101-+111-)+(110-+111-) = = -111+1-1+1-1-+11- = x3x2x1+ x4x1+ x4x2+ x4x3 = x3x2x1+ x4 (x1+ x2+ x3).
После длинных и неочевидных группировок удалось, наконец, получить правильное решение. При числе аргументов более 4-х аналитический метод минимизации не рационален.
1.4. Минимизация полностью определённых булевых функций.
Существует несколько способов минимизации булевых функций. Прежде всего это метод Квайна-Мак-Класки, метод Блека-Порецкого и метод минимизации с помощью карт Карно или диаграмм Вейча [13, 22, 29]. Здесь будет подробно излагаться метод карт Карно, как самый удобный метод, позволяющий быстро решать задачи минимизации булевых функций от достаточно большого числа аргументов (6-12). При этом получается минимальная форма в базисе И, ИЛИ, НЕ.
Существуют карты Карно на 2 , 3 , 4 , 5 и 6 переменных[13,22]. Причем последние стали использоваться достаточно недавно. На рисунке представлены карты Карно для 2, 3, 4, 5 и 6 аргументов.
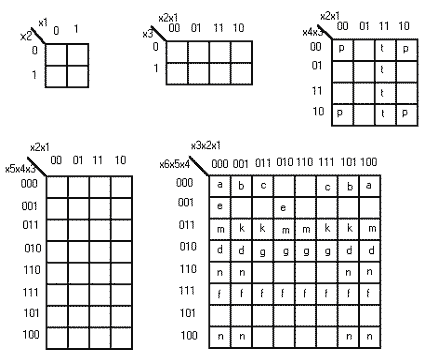
Карты и прямоугольники Карно.
Метод Карно основан на законе склеивания. Склеиваются наборы , отличающиеся друг от друга значением одного разряда. Такие наборы называются соседними. Карно закодировал клетки своей карты так ,что в соседних клетках оказались соседние, а значит, склеивающиеся наборы. Соседними могут быть не только отдельные клетки, которые мы назовем элементарными квадратами Карно, но и целые группы соседних клеток(назовем их прямоугольниками Карно). Под прямоугольником Карно[13] будем понимать некоторую, зачастую разрозненную фигуру покрытия, все соседние клетки которой закодированы соседними наборами. Например, на вышеприведённом рисунке в поле карты для 4-х переменных изображён прямоугольник Карно P, состоящий из четырёх элементарных квадратов Карно, описываемых наборами x4'x3'x2'x1' , x4'x3'x2x1' , x4x3'x2'x1' , x4x3'x2x1' . Если над логической суммой этих четырёх наборов произвести последовательно операции склеивания, то мы аналитически получим результат в виде импликанты (под импликантой будем понимать неполный набор)x3'x1'. Карта Карно позволяет получить этот результат графически значительно быстрее и проще. Для решения этой задачи используем алгоритм графической минимизации.Кстати говоря,сам Карно никакого алгоритма не предложил.
Алгоритм "НИИРТА" графической минимизации булевых функций.
Примечание.
Если в карте Карно нулей окажется меньше чем единиц, то удобнее прямоугольниками Карно покрыть все нулевые наборы. В результате мы получим инверсию минимизируемой функции.
Сущность алгоритма достаточно прозрачна. Стремление к минимальному количеству прямоугольников Карно приводит в результате к минимальному количеству слагаемых в булевой функции. Требование получения максимальной площади прямоугольника Карно вызвано стремлением минимизировать длину каждого слагаемого булевой функции.
Применим карту Карно для решения задачи 1. Возможны два варианта решения.
f = x4x1 + x4x2 + x4x3 + x3x2x1 f' = x4'x1' + x4'x2' + x4'x3' + x3'x2'x1'
Эти выражения представляют собой пример дизъюнктивной нормальной формы (ДНФ).
В некоторых случаях приведение результата минимизации к скобочной форме позволяет уменьшить количество ИС , необходимые для реализации булевой функции. Скобочная форма для f имеет вид:
f = x4(x1 + x2 + x3) + x3x2x1
Карта Карно для решения задачи 1.
